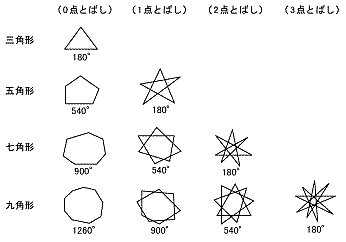
これも星形正五角形と同じ方法でやれます。 奇数の星形は、このように証明すればいいのです。 証明 先の尖った三角形が9個あります。だから、 180度×9=16度 中にある七角形の外角の和が2つ分あります。 360度×2=7度(3) 正五角形では5つの外角の和は ゜だから1つの外角は ゜ したがって1つの内角は ゜です. 何角形でも外角の和は360° この問題は五角形の内角の和が540°になることを使っても求められるが,初めの2つの空欄を埋めるには,問題文で指定された順に答える方がよい.外角は内角の補角である (内角) (外角) =180° (外角) =180°− (内角)

数学 中2 51 多角形の内角と外角の和 基本編 Youtube
八角形の外角の和
八角形の外角の和- (1)正八角形の内角の和は何度でしょう? (2)正八角形の外角の和は何度でしょう? (3)正八角形に対角線は何本引けるでしょう? 解説 (1)内角の和と来たら、どんな三角形でも内角の和は180度と使っていきたいところ。解:根據三角形內角和=180°,可以列出下列式子: 85°33°∠C=180° ∠C=180°−85°−33°=62° ∠C∠1 =180° ∠C外角=∠1=180°−62°=118°




多角形の内角の和 外角の和の公式 数学fun
(1)六角形 (2)八角形 (3)正十二角形 内角の和 内角の和 内角の和 外角の和 外角の和 外角の和 2 内角の和が,次のようになる多角形は何角形か。・星形六角形の頂角の和は,ほとんどの生徒が求めている。 <発表された生徒の解き方> (4) レポート作成の課題を与える。 1) 頂角の和が180度になる星形多角形を調べよう。 2) 星形偶数多角形の性課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を
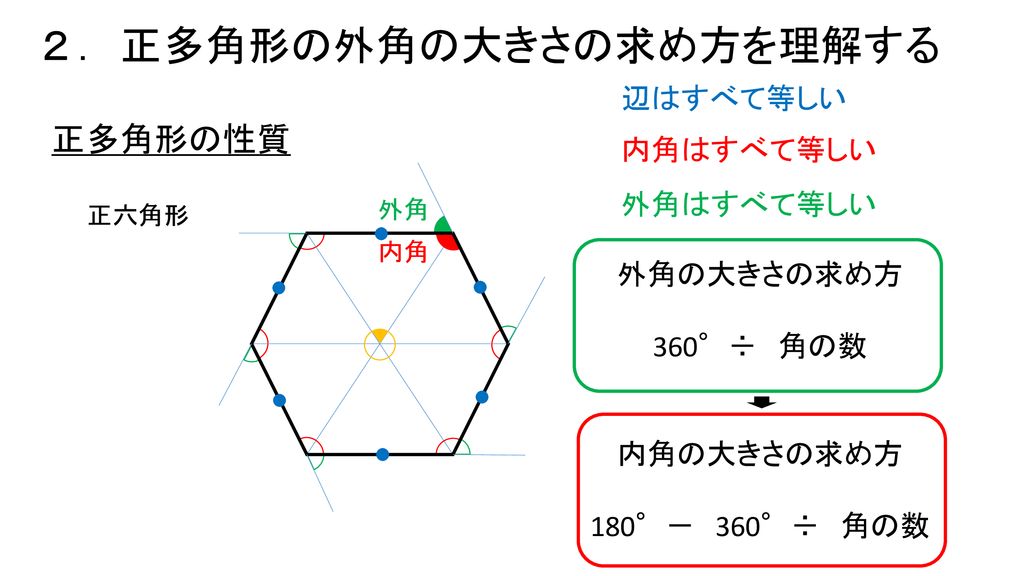
い2つの内角の和に等しい。 1 内角 外角 多角形の内角と外角 ⑴ n角形の内角の和は, 180ß*(n2) である。 ⑵ 多角形の外角の和は 360ß である。 2 3 どんな多角形でも,外角の和は 360ß である。 360ß 360ß チェック3 多角形の外角の和 1正十角形には,内角が10個あります。 なります。 次に,「外角の和」から求める方法を解説していきます。 外角の和は,何角形であっても,必ず360度です。 正十角形も,やはり外角の和は360度です。 正十角形には,外角は10個あります。平行と合同 例題 平行線の錯角・同位角 補助線を引く問題 三角形の内角と外角の関係 印をつけた角の和 角の二等分線と内角の和 三角形の合同証明1 三角形の合同証明2(辺の共通) 三角形の合同証明3(角の
三角形の内角と外角を示しました。 外角と内角の和 外角と内角の和に関する関係は是非覚えましょう。 外角=隣り合わない内角の和 外角隣り合う内角=180度 内角の和と三角形の関係は?1分でわかる和の値、証明、外角との関係 多角形の内角の和は?内角の和・外角の和の証明 なぜn角形の内角の和が180°×(n2)となり、外角の和は360°になるのか見ていきましょう。 内角の和について 多角形の内角の和は小学校のときに習ったと思うので復習にな正十八角形 正十八角形においては、中心角と外角は°で、内角は160°となる。 一辺の長さが a の正十八角形の面積 S は = で、外接円の半径 R は = で与えられる。 (/) を平方根と立方根で表すと、 = = = = = = 正十八角形の作図 正十八角形は定規とコンパスによる作図が不可能な図形で
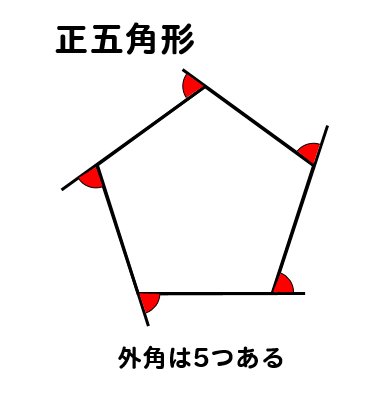



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




4章 平行と合同 2 多角形の外角の和 Ppt Download
出典 フリー百科事典『ウィキペディア(Wikipedia)』 ( 59 UTC 版) 多角形の内角の和/外角の和 n 角形の内角の総和は、多角形の形状に関わらず(凸であれ凹であれ) である。 これはどのような多角形でも、対角線で適当に区切ることで (n2) 個の三角形に分割できることから導かれる。N個の内角とn個の外角の総和は, 180°×n (1) 外角の和は 360° (2) したがって, 内角の和は (1)−(2) 180°×n−360°=180°×(n−2) 図5 (証明 2) 1つの三角形の内角の和は 180° 図6で示されるように, n角形は n−2 個の三角形に分けられるから,内角の和は (n−2)×180°動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



720度 星形九角形の角度の和
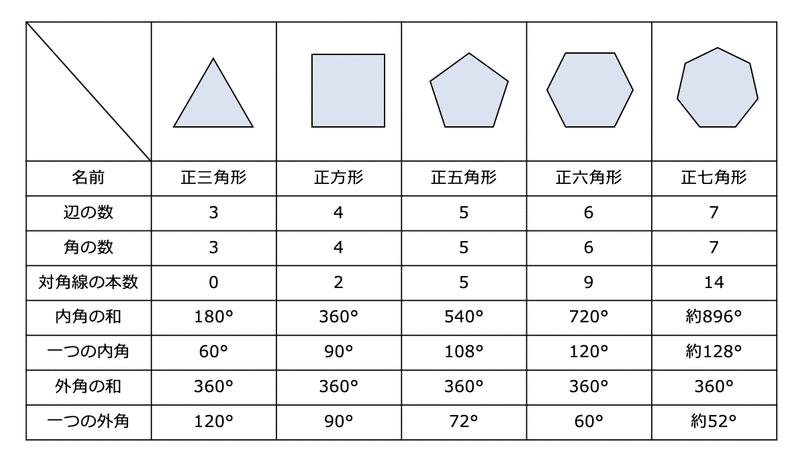



六角形的角度
正八角形の内角の和を求めなさい。 式 答え 正六角形の1つの内角の大きさを求めなさい。 式 答え 正八角形の対角線の数を求めなさい。 式 答え 1つの外角の大きさが°であるのは正何角形か。 式 答え 内角の和が °であるのは、正何角形か。 式 答え八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。; まず1つ目は、 外角の和は常に360°になる ということです。 三角形だろうが、六角形だろうが、百角形だろうが! どんな多角形であっても外角を全部集めて足すと360°になります。 次は、 隣り合う内角と外角の和は180°になる ということです。



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋




多角形の内角の和 外角の和の公式 数学fun
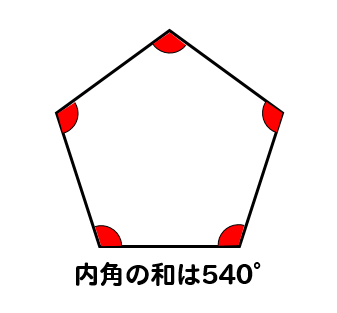
四角形の内角の和: 360° 360 ° 五角形の内角の和: 540° 540 ° 六角形の内角の和: 7° 7 ° ・・・ n角形の内角の和: 180°× (n−2) 180 ° × ( n − 2 ) この公式は覚えやすいので暗記してもいいのですが、簡単に導出できるため、わざわざ覚える必要も4 星形 n 角形の角の和 星形七角形を,内側の七角形の各辺を延長してできた図形と考える。 内側の七角形のまわりにできた7つの三角形の内角の和の合計は, 180°×7=1260° また,七角形hijklmnの外角の和は360°だから,八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。;



2




数学 中2 51 多角形の内角と外角の和 基本編 Youtube
(1)九角形の内角の和は何度ですか。 (2)正五角形の1つの内角は何度ですか。 (3)1つの外角が°の正多角形は正何角形ですか。 (4)六角形の対角線の本数は何本ですか。 (5)下の図のアの角度は何度ですか。(1) 七角形の内角の和を求めなさい。 (2) 1つの内角の大きさが150°になる正多角形は正何角形か求めなさい。 (3) 十八角形の外角の和を求めなさい。 (4) 内角の和が1440°になる多角形は何角形か求めなさ 展开全部 内角和为()×180=1080 外角和是不变的360 如果是正八角形,每个内角就是1080÷8=135 如有疑问,请追问;如已解决,请采纳 54 已赞过 已踩过 < 你对这个回答的评价



2




多角形の性質 第2回 多角形の内角の和の求め方 算数パラダイス
正多角形の内角・外角 まとめ お疲れ様でした! 外角の和は常に360°になる という性質は非常に便利でしたね。 問題でも大活躍する性質なので 絶対に覚えておきましょう。 内角が問題に出てきた場合でも $$\large{(内角)(外角)=180°}$$外角の和を求めることができる。多角形の外角 の和は,⑤ 360° である。 2 多角形の外角について,次の問に答えなさ い。(p92) (1) 八角形の外角の和 多角形の外角の和は360°である。 答 360° (2) 正十角形の1つの外角の大きさ 360°÷10 =36° 答 36°(7) 各自で1つ多角形を決め,その外角の和を求めさせる。指名して式と答えを 発表させ(四角形や八角形,五十二角形など),すべて外角の和が360°にな ることを確認する。 はじめに計算が簡単な四角形や八角形を扱い,その後に五十二角形を扱う。



正5角形の角度の求め方は 1分でわかる値 内角の和 正6角形 正8角形の角度は




1 2 31 4 1 5116 6 Lihat Cara Penyelesaian Di Qanda
(4) 十八角形の外角の和は何度か (5) 内角の和が2340°である多角形は何角形か。 (6) 内角の和が1800°である多角形は何角形か。頂点とする三角形の角の和から五角形の外角の 和を2つ分ひき,180°と求めることができる。 B ①では,図形の性質を利用することで星型五角形 の内角の和を演繹的に求める例をあげた。では, 結ぶ点の数を増やしたときに内角の和はどうな るだろうか。(3) 正十角形の1 つの外角の大きさを求めなさい。 「外角」についての問題は、『多角形の外角の和は(何角形でも必ず)360°である』ということを利用! ( 36° ) (4) 1 つの外角が24°である多角形は正何角形か。 360°の中に24°はい



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



子供からの質問です 正八角形の一つの内角の大きさと 対角線の数を求めなさ Yahoo 知恵袋
5年以上前 正多角形の外角の和って360度ですね。 という事は、正三角形の一つの外角は360÷3 正方形の一つの外角は360÷4 正五角形の一つの外角は360÷5 というようにしていけば 。 5年以上前 ありがとうございます性質3六角形について, (5 つの内角の和) =(他の1 つの外周角)+360° すなわち,a+b+c+d+e=F+360° 性質3 も,性質2 の証明1 や証明2 と同じよ うに証明できる(詳細は略)。 さらに,七角形,八角形,を調べると,次 の通りである。 <七角形の場合>




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




多角形と外角の和 Youtube



Http Www Pref Osaka Lg Jp Attach 6629 Jmw 2b4 3 Pdf




多角形の内角の和の公式と外角の和を利用した角度の求め方



2




中学2年の数学 動画 多角形の内角と外角の和 計算編の問題 19ch



Cmsweb2 Torikyo Ed Jp T Chu Kyou Shin Action Common Download Main Upload Id 112



Fzk Ed Shizuoka Ac Jp Shizuchu Wp Content Uploads Sites 4 17 02 5b4511dfa47fa1a398d0591ccee2 Pdf



2




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和の公式 数学fun




正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear



1




なんで かっこ1番nー2 15なんですか Clear



1




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




1つの内角の大きさが 1つの外角の大きさの8倍である正多角形を答えなさい この問題の Clear




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
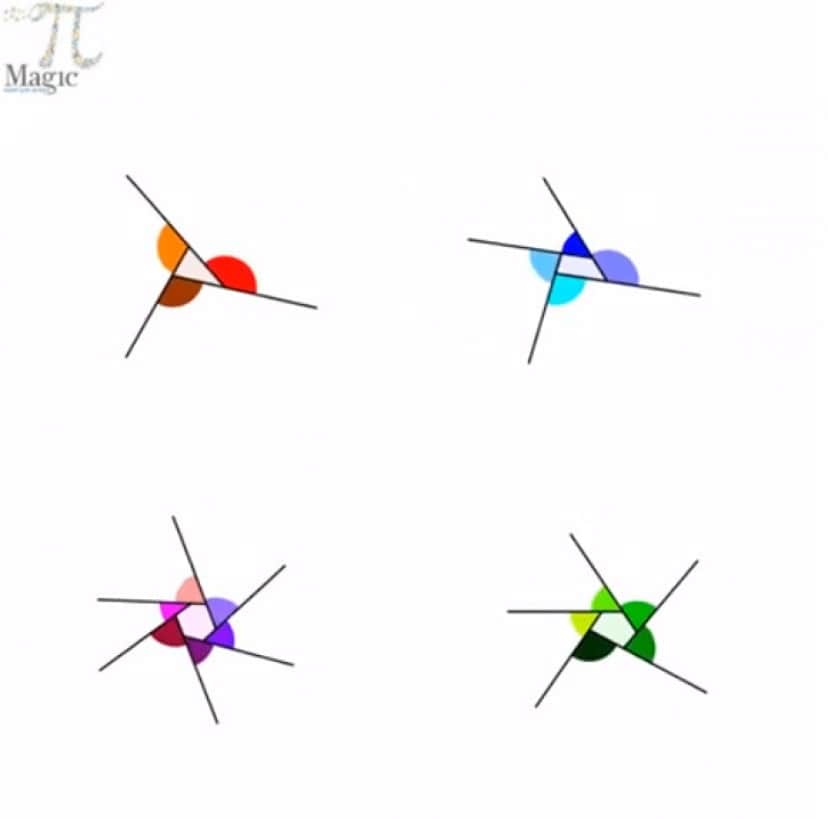



多角形の外角の和は360度 をgifアニメで表現 これがわかりやすいと海外で話題に カラパイア




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
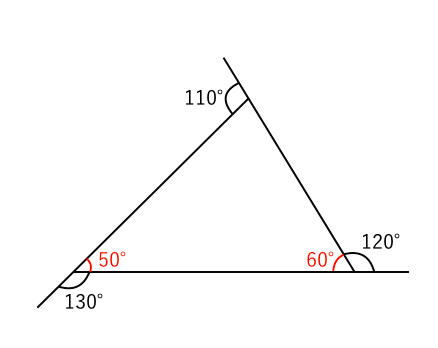



図形の調べ方 外角を求める 苦手な数学を簡単に
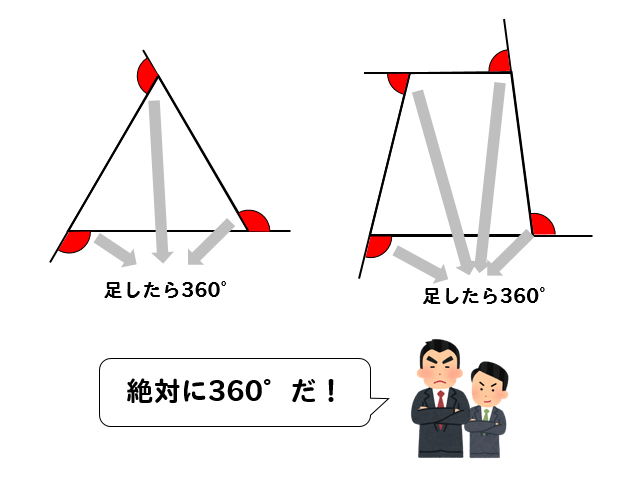



正多角形の1つの内角 外角を求める方法を問題解説 数スタ
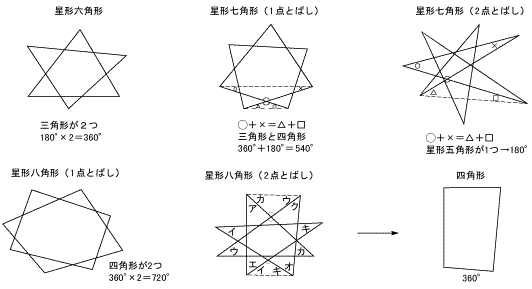



課題学習の指導 数学




正多角形の1つの内角 外角を求める方法を問題解説 数スタ



中2数学 多角形の内角の和 外角の和まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
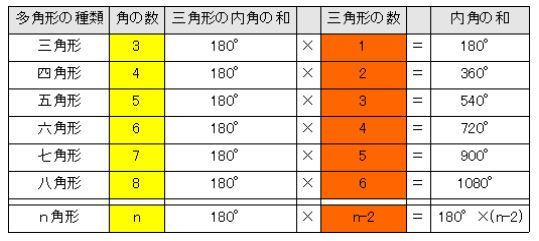



内角攻め それとも外角攻め すうがくラボのブログ




正多角形の内角と外角の大きさ 具体例で学ぶ数学
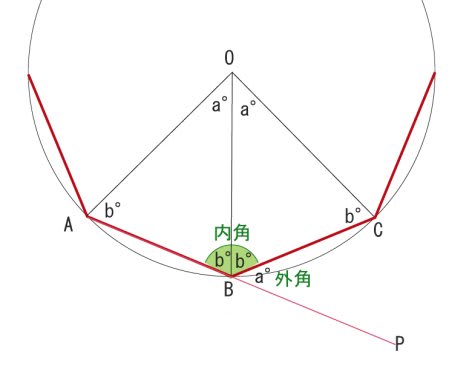



内角 外角 180 どうして 名寄 算数数学教室より
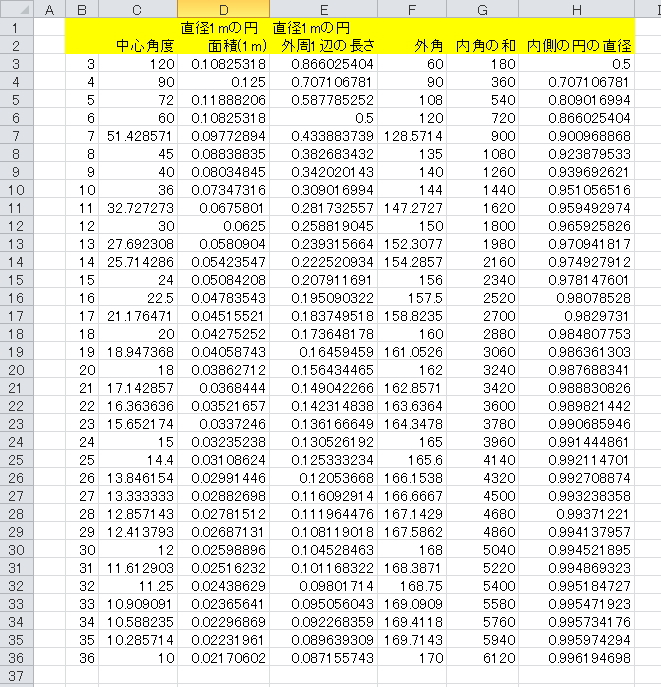



正 角形 正多角形 を表にしてみる エクセル関数の使い方




小学校5年 算数 正多角形の角の大きさ Youtube



3



図形の調べ方 N角形について 内角の和を求める 苦手な数学を簡単に




一つの内角が160度である正多角形は正何角形ですか Clear




十八角形 Wikipedia




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



正8角形 正八角形 の角度の求め方は 1分でわかる内角の和 計算 外角 正9角形の角度




多角形の内角の和 外角の和の公式 数学fun



1



Http Hokusuukyou Cyuu Com 17 2 Zukei Pdf




外角 多角形
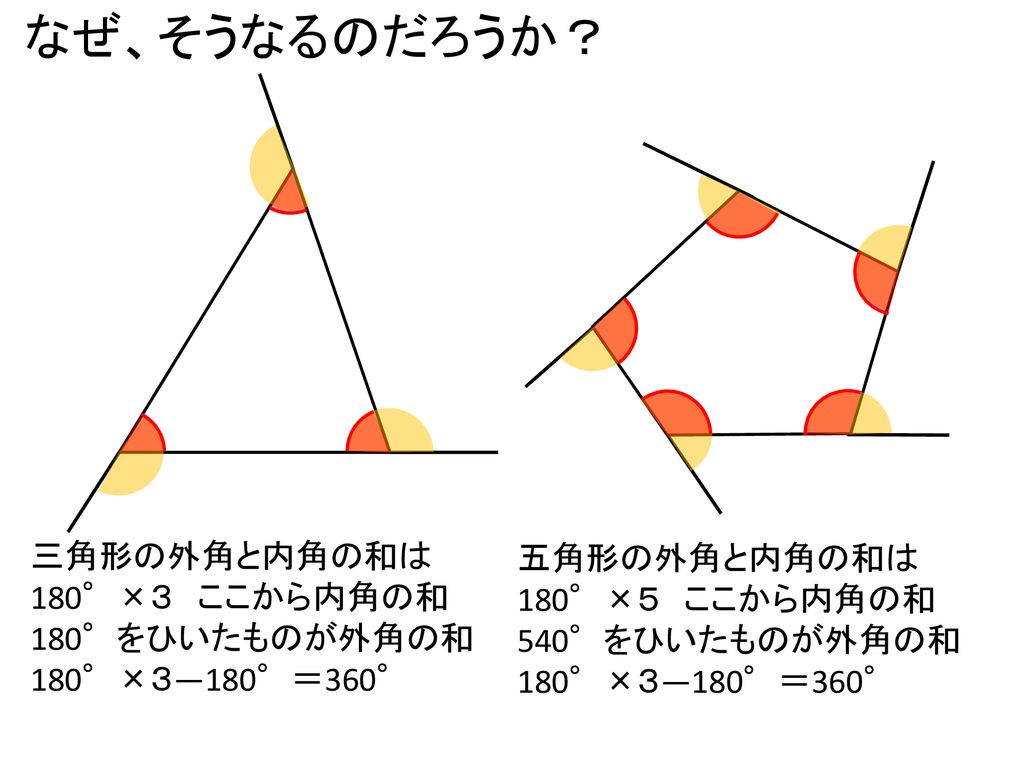



多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download




内角の和 180 N 2 外角の和 360 教遊者



720度 星形九角形の角度の和




無料 中2数学 基本解説 解答プリント 223 図形3 多角形の角




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく
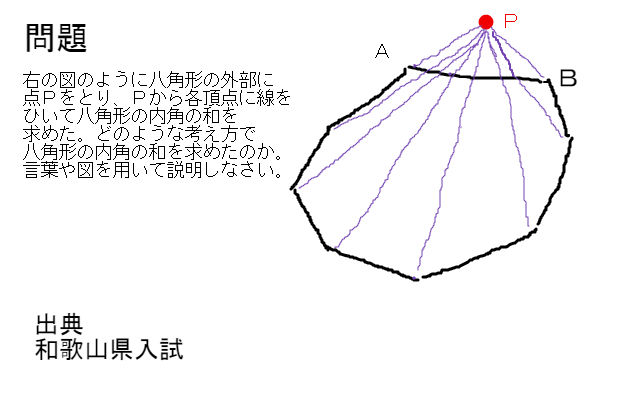



図形問題の徹底演習 八角形の内角の和 中学数学 理科 寺子屋塾の復習サイト



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




無料 中2数学 基本解説 解答プリント 227 図形7 復習




図形問題の徹底演習 八角形の内角の和 中学数学 理科 寺子屋塾の復習サイト



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



みんなの算数講座 第31講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん




内角の和 180 N 2 外角の和 360 教遊者



Http Www Fukui City Ed Jp Meido J Pdf 2 3 2 4 Pdf
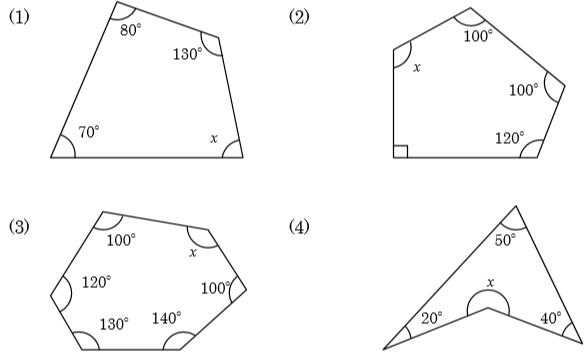



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu




多角形の内角の和 外角の和の公式 数学fun




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



Http Www Asahikawa Hkd Ed Jp Nagayama Jhs 221 Ef 92 E5 B9 B4 E6 95 B0 E5 Ad A6 Ef E5 9b E5 80 80 E5 9a E8 92 E5 81 Ae E5 86 85 E8 92 81 A8 E5 96 E8 92 80 80 E8 A3 E7 Ad 94 Ef Pdf
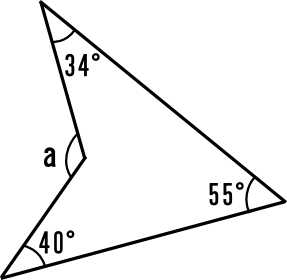



中学2年数学練習問題 図形の調べ方 多角形の内角と外角の解答



多角形の外角の和 On Vimeo
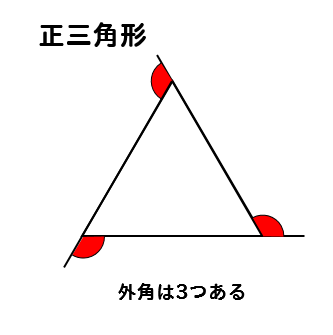



正多角形の1つの内角 外角を求める方法を問題解説 数スタ
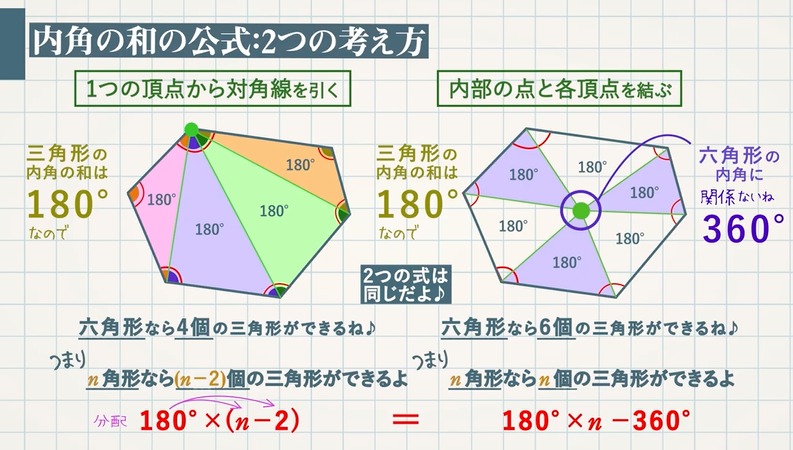



内角の和 180 N 2 外角の和 360 教遊者




内角の和 180 N 2 外角の和 360 教遊者
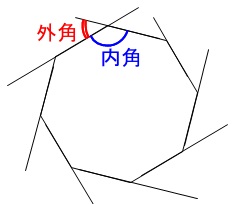



多角形の内角の和の公式と外角の和を利用した角度の求め方




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




内角の和 180 N 2 外角の和 360 教遊者



Mathematics 算数のコツ 1 角度の問題は 等しい角を見つけて書き込む 働きアリ The 2nd
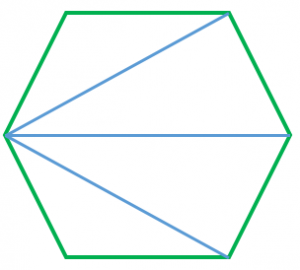



正多角形の内角と外角の大きさ 具体例で学ぶ数学




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



Fzk Ed Shizuoka Ac Jp Shizuchu Wp Content Uploads Sites 4 17 02 5b4511dfa47fa1a398d0591ccee2 Pdf
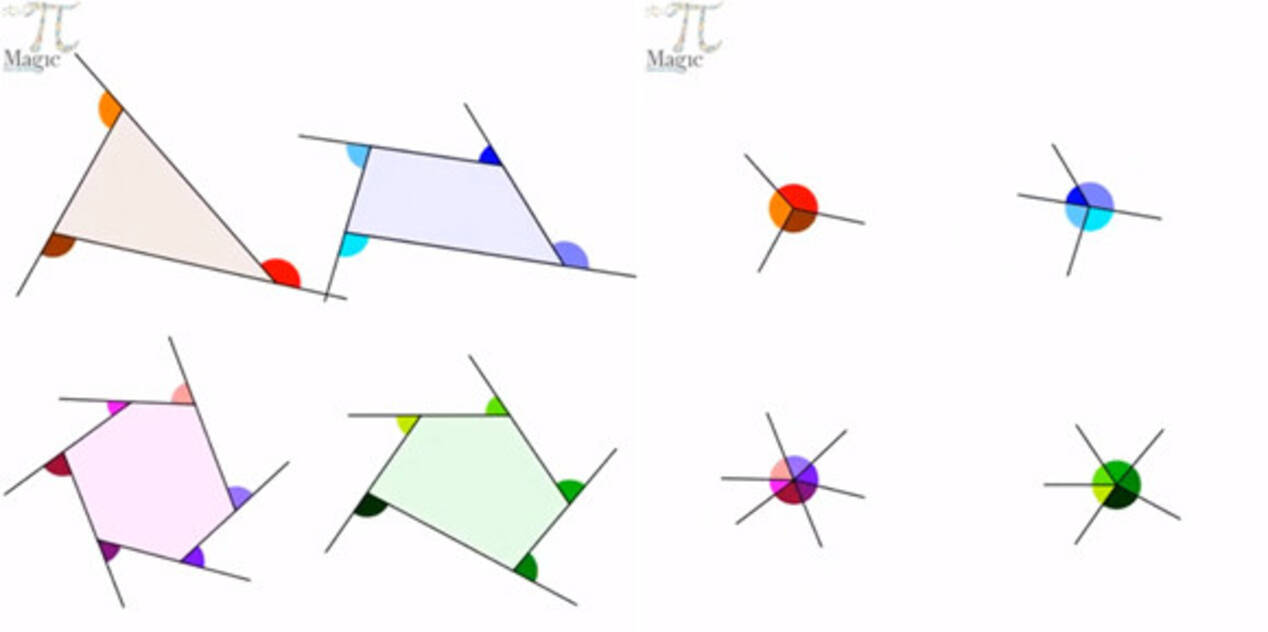



多角形の外角の和は360度 をgifアニメで表現 これがわかりやすいと海外で話題に 19年5月22日 エキサイトニュース



みんなの算数講座 第31講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん
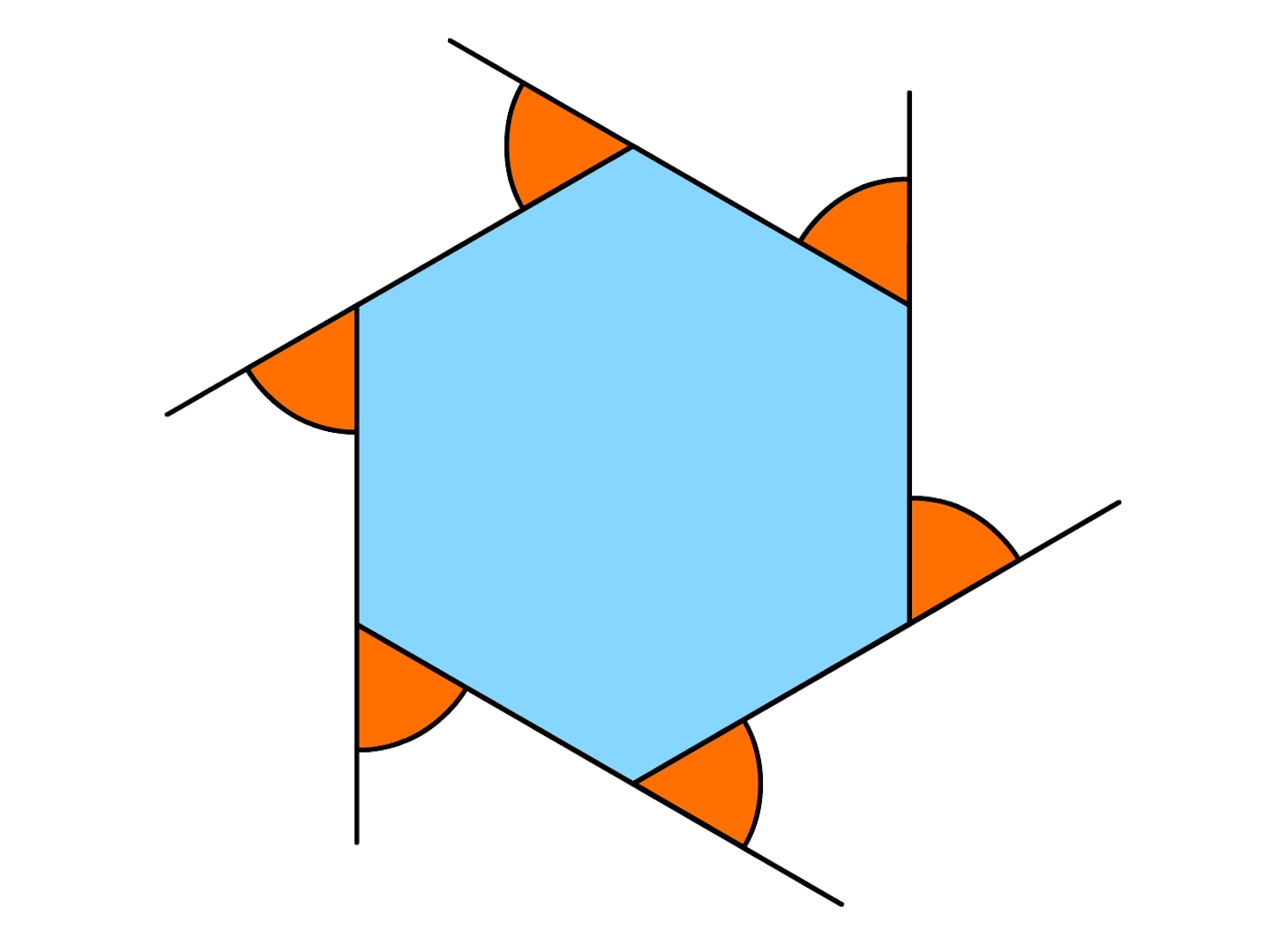



2年 多角形の外角 数学イメージ動画集 大日本図書



課題学習の指導 数学




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形の外角の求め方を5分でサクッと理解 中学数学 理科の学習まとめサイト
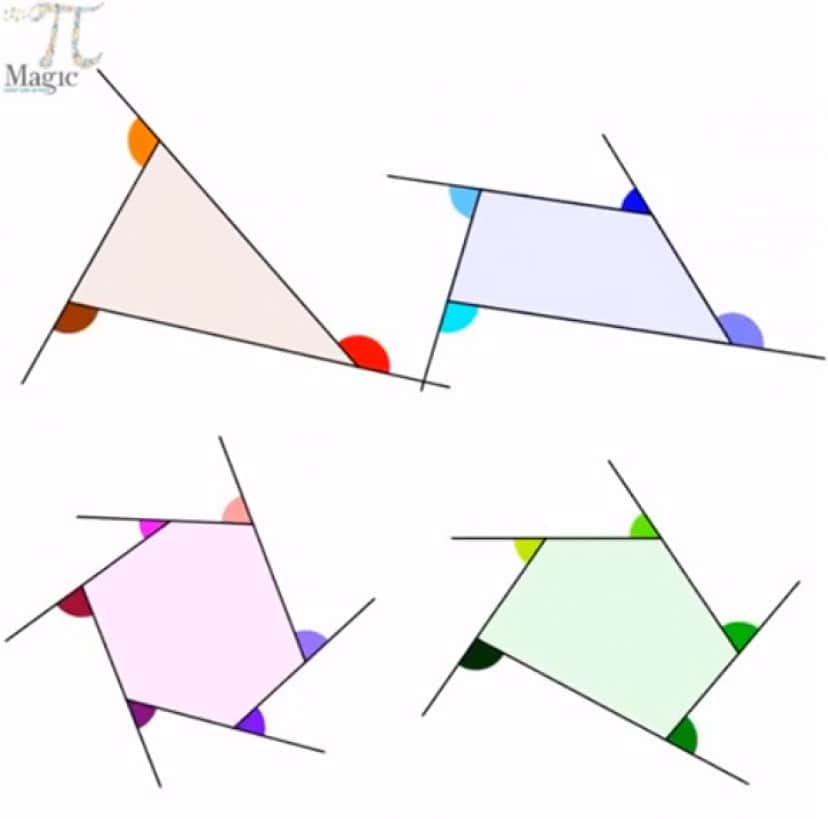



多角形の外角の和は360度 をgifアニメで表現 これがわかりやすいと海外で話題に カラパイア



720度 星形九角形の角度の和




中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu
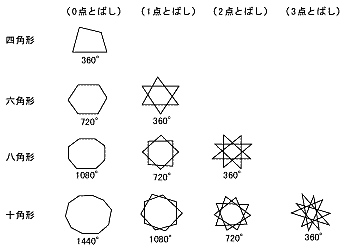



課題学習の指導 数学



多角形の内角と外角 思考力を鍛える数学



南山中学女子部過去問題演習




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



多角形の外角の和 勉強ナビゲーター
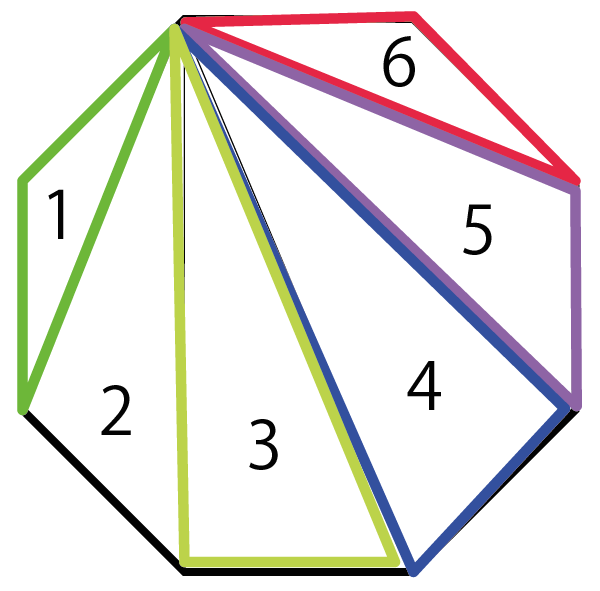



3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




課題学習の指導 数学



Www City Hadano Kanagawa Jp Www Contents Simple C050a Pdf




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿