今回は中2で学習する 『連立方程式』の単元から 連立方程式を代入法で解く方法について解説していくよ! 連立方程式を解くためには 『加減法』と『代入法』という2つの解き方があったよね。 &nbs4 同次形の解き方・注意 {5{ 同次形の方程式 y′ = f (yx) 変数分離形の解き方と同様に f(u) u = 0 を満たす値u = mが存在するとき問題が起こる。 u = y=xなのでy = mx (直線)となる。 実際にこのとき y′ = m;連立線形微分方程式 {x ′ = ax by y ′ = cx dy について いずれか一方の関数の線形2階斉次微分方程式に帰着させて解くことができるようになります。 微分演算子を用いた表現により,連立方程式を解くことができるようになります。 係数行列の対角化に
至急お願いします この連立方程式が解をもつように定数kを定 Yahoo 知恵袋
連立方程式解き方 xyz
連立方程式解き方 xyz-F (yx) = f(m) = m となってy = mxは同次形の方程式の解になっている。 多くの場合はy = mxは一般 と連立方程式に苦戦している方のために、「 連立方程式の解の3パターン(解あり、任意の解、解なし) 」をそれぞれ分かりやすく解説します! ついでに同次形の連立方程式の解法も最後に説明しているので良かったらご覧ください。




掃き出し法を用いた連立1次方程式の解法と例題 Avilen Ai Trend
STEP1 連立方程式の解き方~加法~ 問題です。 この連立方程式を解け。 連立方程式を解くには未知数に注目するのがポイントです。 xかy第12章「微分方程式」の問題 例題12-1 dy dx = −xy2 を解け (例題12-1の解答)変数分離形であるので変形して両辺を積分する と, Z − 1 y2 dy = Z xdx y = 2 x2 C (C は積分定数) 類題12-1 以下の変数分離型微分方程式を解きなさい (1) dy dx = exy (2) dy dx = xy (3) dy dx連立方程式の作り方の考え方としては・・・ A町から峠までの道のりを x km、峠からB町までの道のりを y kmとします。 1つ目の式は『行きの時間』の式で『A町~峠の時間+峠~B町の時間=15時間』となります。 式1 x 3 y 6 = 15
プライバシーポリシー 免責事項 19–21 方程式の解き方まとめサイト 免責事項 19–21 方程式の解き方まとめサイト連立方程式を解く 連立方程式を解くには,xかyのどちらかの文字を1つ消去して,文字が1つだけの方程式にして解く。 この解き方に加減法と代入法がある。 加減法 x,またはyの係数をそろえて2つの式を 「たす」または「ひく」して文字を一つ消す。Xyz3つの式の連立方程式の解き方がわかる4ステップ xyzの3つの文字がはいった連立方程式の解き方を解説してみました。よかったら参考にしてください。 4y = 8 y = 2 になるでしょ。 これでyの解もゲットできたね! Step4 文字を2つ代入しちゃう!
連立方程式の解き方 (代入法) 連立方程式とは2つの文字 (xとy)を含み、2つの式からなる方程式のこと。 連立方程式の解き方には 代入法 と 加減法 がある。 どちらの場合もxかyのどちらか 1つの文字を消さて、ここまで来れば方程式の計算マスターまであと一歩です。 例5 次の方程式を解きなさい。 小数の項が両辺にある場合は、両辺に10や100をかけて、すべての項を整数にしてから計算します。 また、両辺に分数がある場合は、分母の最小公倍数を 1 はじめに 2 連立方程式の解き方のすべての基本! 「代入法」と「加減法」 21 連立方程式の解き方基本:加減法 22 連立方程式の解き方基本:代入法 23 連立方程式「x2y = 2xy9 = 11」の解き方 24 文字が3つ出てくる連立方程式の解き方 3 文字同士のかけ算が入る連立方程式の解き方 31 連立方程式は「いかに簡単な計算をするか」を考えよう




連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




連立方程式 3つの文字 式の問題を計算する方法は 数スタ
2 回答 xyが分母にある 連立方程式の解き方を教えてくだい。 15/ (xy)12/ (4x3y)=11・・・① 3/ (xy)2/ (4x3y)=2 ・・・・② です。 両辺に(x-y) (4x3y)を掛けてやろうとしましたが、 挫折しました よろしくお願いします。 xyが分母にある 連立方程式の解き方を教えてくだい。 15/ (xy)12/ (4x3y)=11・・・① 3/ (xy)2/ (4x3y)=2 ・・・・② です。 両辺つまり、式にして表現すると以下のようになります。 xy= 2x4y=60 あとは、連立方程式の解き方と同じように解いてください。ただし、xやyが何を指しているのかを忘れないよう! さいごに 連立方程式は、中学校で習った範囲です。の値が分かっているのだから,それらを連立方程式に代入すると成り立つはずです. このときできるのは, の方程式ではなく, の方程式です.この の連立方程式を解きます. に数字を代入しているのだから,もう は残っていません.



Excel の行列計算による連立方程式の解き方




連立1次方程式が 解をもつ条件 と 解の自由度 の考え方
3元連立方程式ですね。 パターン1 xy=a yz=b xz=c となっている場合 全ての式を足して、2 (xyz)=abcxyz= (abc)/2 xyzの値がわかったので、この式から、各最初の3つの式を引くと、x,y,z各値がわかる。大人の解き方(連立方程式)-誰でも解ける機械的方法 まず大人(中学生以上)はこれをどう解くか。連立方程式を用いて、きわめて簡単に解くだ ろう。すなわち、求めたい姉と妹の所持金をそれぞれx、yとすると、 4/7x+2/3y=7400 (1) (a) 対称式の連立方程式の解き方 普通に解けそうならそのまま解く 無理そうなら、 (和) = a, (積) = b ( 和) = a, ( 積) = b とおいて a, b a, b の連立方程式を解く 2次方程式 t2 − at b = 0 t 2 − a t b = 0 を解く ステップ2で x y = a, xy = b x y = a, x y = b とおいて a, b a, b を求めたので、 x y, xy x y, x y の値がわかったことになります。 ステップ3では、ここから x, y x, y を



Iseqi Pukiwiki



Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
中学数学や、 高校数学を楽しむのが、 「答えを作り出す」、あるいは、 「答えを生み出す」解き方です。 そして、 「答えを作り出す」、あるいは、 「答えを生み出す」解き方に、 子どもを導くことができる計算は、 連立方程式です。 経験から生まれた仮説です。連立方程式 列車 すれ違い 9 xy=3,xy=2の和と積の連立方程式の解き方は? 途中で速さが変わる文章問題の解き方、コツを解説! 割合を使った全校生徒の増減に関する文章題の解き方を解説! 池の周りを追いつく速さの問題を解説! 中2数学, 今回は、連立復習連立方程式の解き方 連立方程式とは、一般的に \begin{eqnarray}\left\{\begin{array}{l}axby=c\\dxey=f\end{array}\right\end{eqnarray} といった形で表すことが多い式です。 2元1次方程式と呼ばれる「2つの変数(文字)」と「最大次数が1」の式で表




行列と連立方程式について 以下の画像の問題です 1 は示すことが出 Okwave



Http Polymer Chem Bio St Gunma U Ac Jp Renritu Pdf
連立不等式の解き方と共通範囲について|+数直線の書き方も解説 つまづく高校生が続出する「連立不等式」ですが、難しく考える必要はありません。 解き方はシンプルでして、やるべきことは2つだけです。 連立不等式の解き方 手順①:それぞれの不加減法による連立方程式の解き方 一方の文字(xまたはy)の係数の絶対値をそろえ,連立している2つの方程式の左辺どうし, 右辺どうしを加えたり,またはひいたりして文字を消去し,連立方程式を解く方法を加減法とい う。 3 加減法による連立方程式の解き方方程式を解くに当たって基本となるのは、 移行・同類項の計算・左辺を文字のみにする の3つです。 まず移行ですが、 x が付いている数字( x の項と言います)を左辺に、 x が付いていない数字を右辺に移動します。 このとき注意しなければいけないのは、左辺から右辺もしくは右辺から左辺に移動する数字に関しては符号が変わるという点です。 10 x 4 = 2 x 12 10



連立方程式 1 代入法と加減法 バカでもわかる 中学数学




掃き出し法を用いた連立1次方程式の解法と例題 Avilen Ai Trend
連立方程式の解き方の基本となる加減法の問題とポイントの説明です。 加減法とは連立方程式の解き方の1つですが、これだけでも通用するのでしっかり身につけておくと良いです。 中学数学では連立方程式の文字(未知数)が2つあります 方程式とは?ねらい ・ 連立方程式を進んで解こうとする。 ・ 連立方程式を解くには、既習である文字1つの方程式を導けばよいことに気付くことがで きる。 ・ 加減法による連立方程式の解き方(2つの式をたしたりひいたりして解く)を理解する。 段階 学習活動連立方程式の代入法は、片方の式を ax=byc か by=axc の形にして、もう片方の式に代入し値を求める方式です。



Maximaの方程式 Maxima入門 Maximaのインストールから簡単な数式 グラフ作成まで




特殊な形の連立方程式の解き方 大学受験のための高校数学
連立方程式の解き方には代入法と加減法の2種類があります。 代入法 代入法とは、 「一方にもう一方の式を代入することで文字を一つ消去し、連立方程式を解く方法」 です。 たとえば以下の連立方程式を代入法で解いてみこのページでは,次のような形の連立方程式を 2次-2次連立形 と呼ぶことにします. x 2 y 2 3xy=5 (1) x 2 y 2 −xy=1 (2) このページでは,主に2次2次連立形の連立方程式の解き方を解説します. なお,1次2次連立形の連立方程式は,しばしば登場するもので,必ず解けなければなりませんが,2次2次連立形の連立方程式は教科書や授業ではほとんど触れません 代入法を使って解こう! 連立方程式の解き方には 加減法 2つの式を足したり、引いたりすることで文字を消して計算を進める方法 代入法 式を代入することで、文字を消して計算を進める方法 というものがありましたね。 参考記事 連立方程式代入法の解き方をわかりやすく問題を使って徹底解説!




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ




書記が数学やるだけ 39 行列の階数 連立方程式 1 掃き出し法 Malinka書記 Note
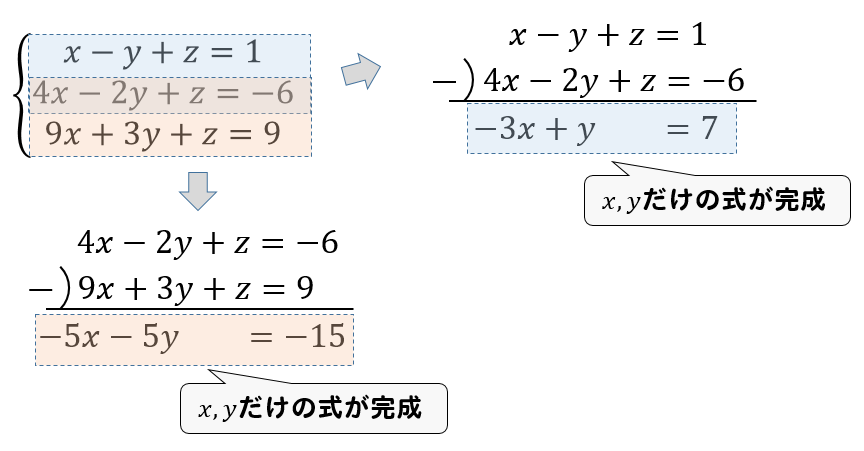
この、分数の文字を別の文字で置き換える解き方は、 分母に文字がある連立方程式ではよく使う よ ただし! 1 x − 1 y = − 5 2 1 x − 1 y = − 5 2 ― , 8 x−2 2 y1 = 10 8 x − 2 2 y 1 = 10 ― であるとき、 x,y x, y の値を求めよ。 みたいに、 と で 分母が異なっ連立方程式を解いてみよう解説 (1) { 3 x y = 18 x y = 10 yの係数が+1で同じですので、そのまま上の式から下の式を引いて、 = 2 x = 8 として xを先に求めます。 x=4,y=6 (2) { 2 x 4 y = 22 2 x y = 10 xの係数が+2で同じですので、そのまま上の式から下の式を引いて、 = 3 y = 12 として yを先に求めます。 x=3,y=4 (3) { 4 x y = − 3 2 x – y = − 92 3つの式、文字がある連立方程式の解き方 21 手順① 1つの文字を消し、2つの文字の連立方程式を作る;



Q Tbn And9gcrxeqtkfzspr84pbplx9xl09lwn 7v64y00sc7qxffojd2h H0u Usqp Cau




X Y Z 3つの式の連立方程式 21年5月17日 鈴木貫太郎 Official Website
不定方程式とは $\ 2x3y=100,\ xyxy=0\ $といった 解が無数に存在する方程式を不定方程式 といいます。 しかし、この方程式に整数解という条件をつけると解が有限個になったり、解は無限にあるけれどもその形が決まったりします。連立方程式1 D SML01 次の各問いに答えなさい。ただし,解答用紙には答えだけでなく,解き方も示すこと。(配点 50) x次の①~③の連立方程式のうち,解が =-2,y=-3 であるものはどれですか。 番号で答えなさい。




やさしい連立方程式を解こう 身勝手な主張



方程式 不等式 恒等式を総まとめ 重要記事一覧 受験辞典




数学ができる新卒は基礎を解説してみたかった 行列の計算 Sios Tech Lab




勉強しよう数学 無数の解がある連立方程式の高校生の解答




2分動画 3元対称式の条件を満たすx Y Zが実数である条件 数学ii 複素数と方程式 Youtube



1



U9j580gf8iba369ji2w Xyz P 1058




中2 連立方程式の この解き方教えて下さい Clear



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト



未知数が x y z の3つの連立方程式です y に付いている数 係数 だけを2倍にすると y の答えは どうなるでしょうか 計算が得意な子に育てる効果的な教え方




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




1 Begincasesxyz2x2y Z53x Yz14endcases クァンダ Qanda で解き方を見る




Deadliner デッドライナー 創作同盟 Digitalart Artistontwitter 一次創作 春の創作クラスタフォロー祭り 数1 受験勉強 勉強垢 大阪大 必要条件 十分条件 Requirements Sufficient Oc 補足 L M Nを設定して解と係数の関係の連立方程式を立て
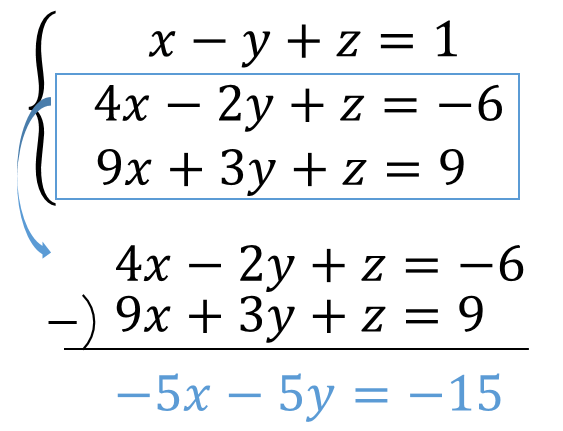



連立方程式 3つの文字 式の問題を計算する方法は 数スタ




整数解をもつ連立3元2次方程式を解こう 2017年度前期日程の一橋大学入試問題 身勝手な主張
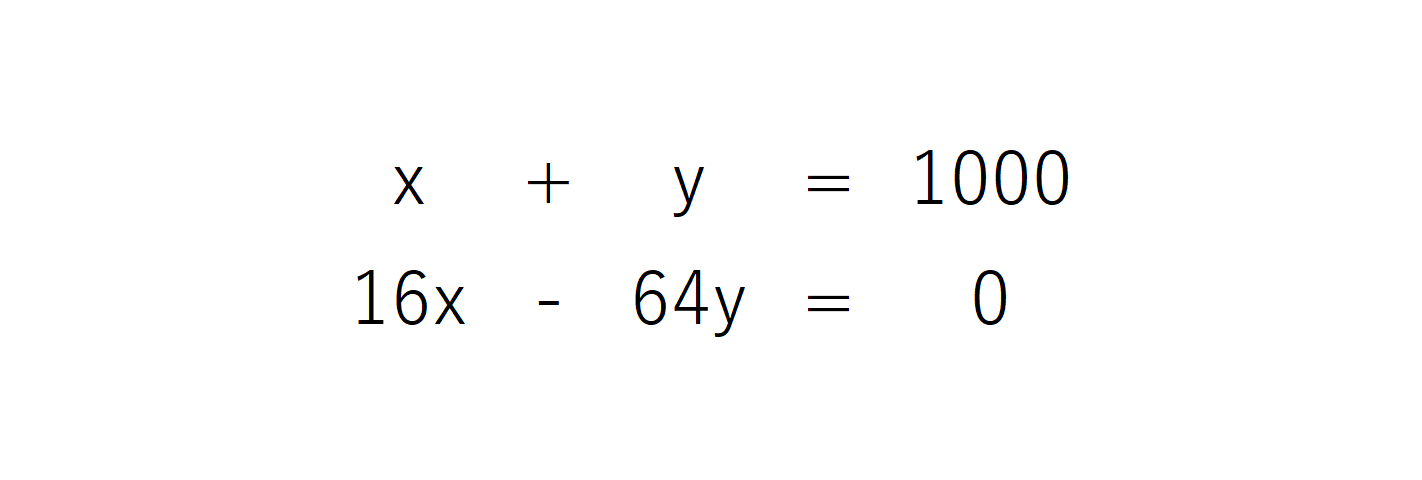



Excel関数 連立方程式 1次方程式 を解く方法 ふみの会社経営日記




やさしい連立方程式を解こう 身勝手な主張



2




高校数学 対称式の連立方程式 対称性を崩さずに求めよ 受験の月



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス




3分でわかる 連立方程式の代入法と加減法をわかりやすく 合格サプリ



13年センター試験数学 B 第1問 その2 ほのぼの数学頑張ろう



連立方程式 下の写真の絵の式 がx Y Z 0以外の解を持つaを定め Yahoo 知恵袋



連立一次方程式について 実数を係数とする次の連立一次方程式が少なくとも Yahoo 知恵袋



U9j580gf8iba369ji2w Xyz P 878



Icu Hsuzuki Github Io Science Class Ns1b Lecnote 08 3 Linearalgebra Pdf




例題演習 クラメルの公式を使って連立方程式を解く 宇宙に入ったカマキリ



至急お願いします この連立方程式が解をもつように定数kを定 Yahoo 知恵袋
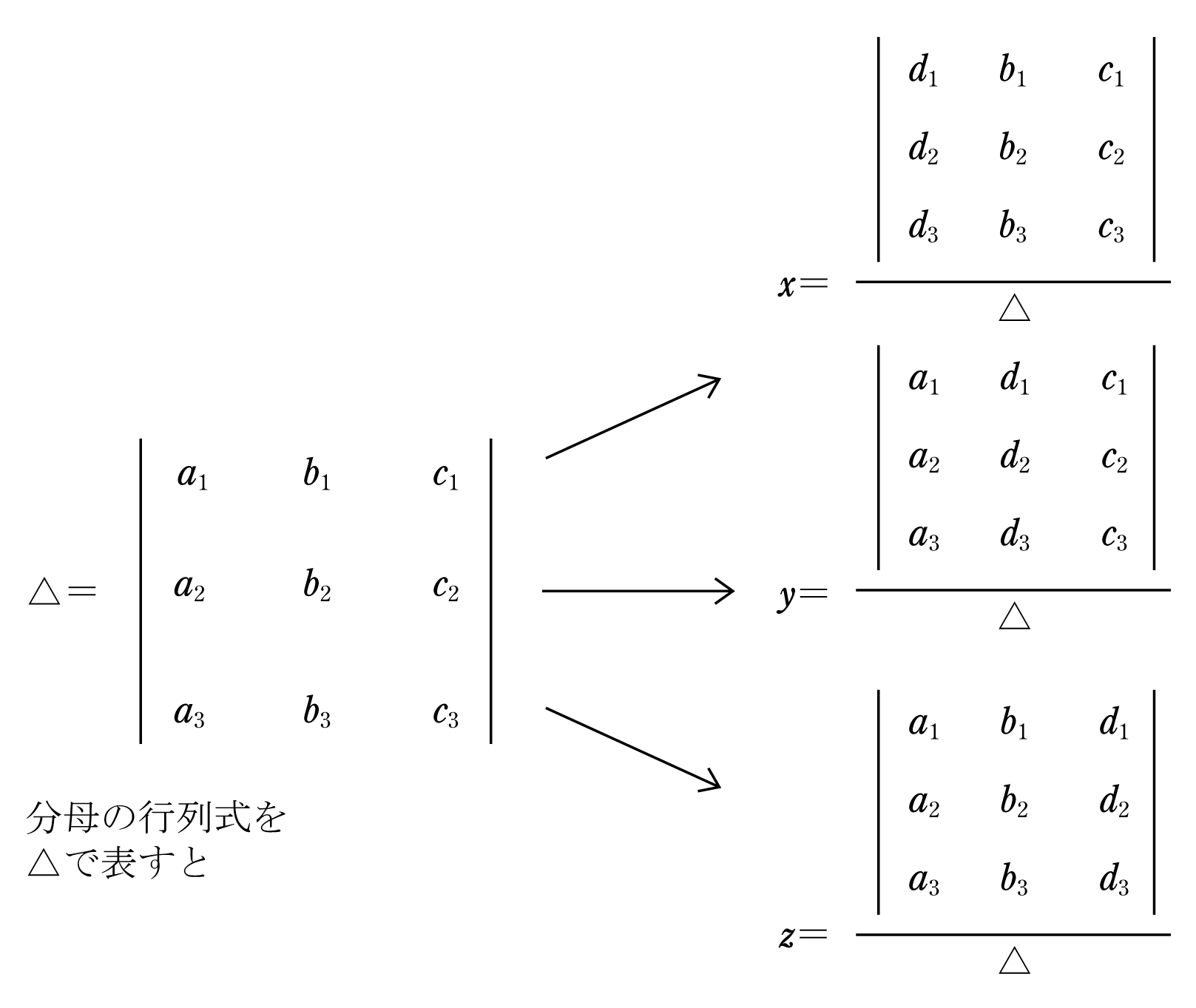



連立方程式と行列式 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会




未定係数を含む3元連立方程式の解 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




三次方程式の解と係数の関係を使う式の変形 2018年度前期日程の静岡大学教育学部 農学部等入試問題 身勝手な主張




りんだろぐ Rindalog 行列で解く Systems Of Linear Equations




しょうちゃん 公式ブログ この計算できますか No 156 連立方程式 クラメルの公式 行列 Powered By Line
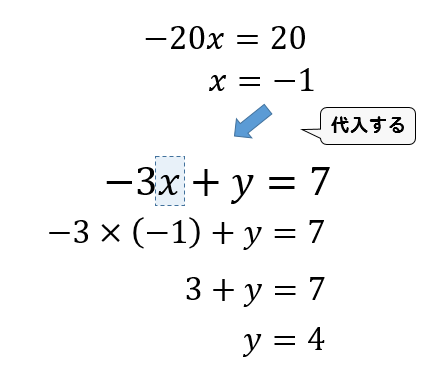



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



Seqi Pukiwiki




中2 数学 連立方程式 Clear




特殊な形の連立方程式の解き方 大学受験のための高校数学




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




連立方程式と式の値 2通りの解法 Youtube




連立方程式とは サイエンスの人気 最新記事を集めました はてな




線形代数 連立方程式 解が無数 写真の式は解が無数に存在します それぞれ Okwave




不定方程式の新着記事 アメーバブログ アメブロ



文字が3つの時の連立方程式の解き方教えてください 二元の連立方程式 Yahoo 知恵袋




3つの連立方程式の問題 解き方はこのようにすればバッチリだ 中学や高校の数学の計算問題




整数解をもつ連立3元2次方程式を解こう 2017年度前期日程の一橋大学入試問題 身勝手な主張



次の連立一次方程式がx Y Z 0以外の解を持つようにaの値を定めよ その時 Yahoo 知恵袋




4元連立方程式の解き方を教えてください 1 x y z W 2 2 x 数学 教えて Goo



2元連立方程式 公文 シモネタ




連立方程式 1 代入法と加減法 バカでもわかる 中学数学



Kadai5



連立1次方程式の掃き出し法と行列の基本変形




超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく
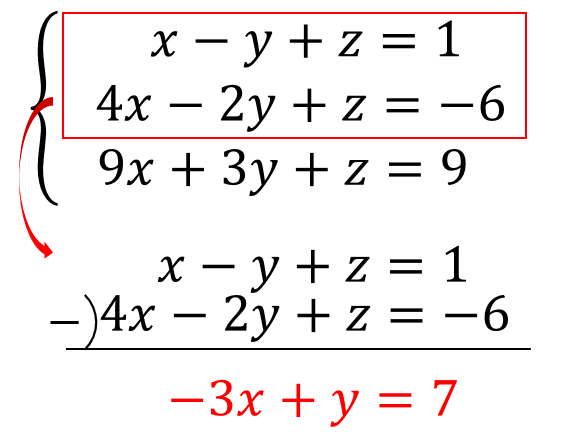



連立方程式 3つの文字 式の問題を計算する方法は 数スタ



U9j580gf8iba369ji2w Xyz P 703



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス




ラグランジュの未定乗数法で計算しているとこのx Y Z Lについての連立方程式をどう Clear




不定方程式の解き方とは 全4パターンを東大医学部生がわかりやすく解説 東大医学部生の相談室



Fdkyb3b9c093sr81e Com E8 A3 E6 9e 90 E5 Ad A6 E9 80 A3 E7 Ab 8b E5 Be Ae E5 86 E6 96 B9 E7 A8 8b E5 8f



連立方程式の未知数が4つでも 係数を見比べることで 解く前に解き方を決める子に育てることが可能です 計算が得意な子に育てる効果的な教え方



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス
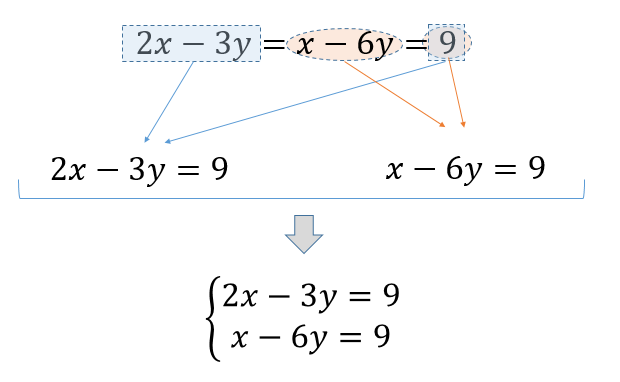



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト



連立方程式とは サイエンスの人気 最新記事を集めました はてな



Http Www Din Or Jp Saigou Math Tyuu2 Pdf




自作数学問題bot Mathquestionakt 問題23 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信
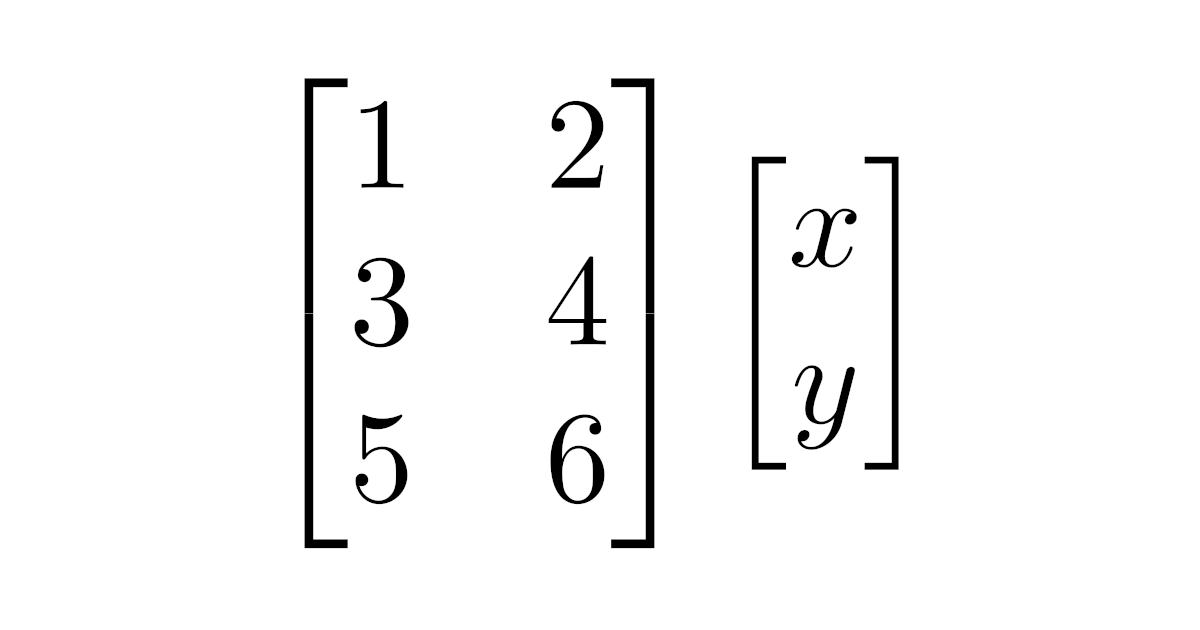



連立1次方程式の掃き出し法と行列の基本変形




中2 2章 連立方程式 解の比 中堅校以上 テストで80点以上取りたい人 向け Youtube




シロバナタンポポ 本日は 数学の 全部応用問題 にて 比を求めることについて解説します Youtubeチャンネル シロバナタンポポ の T Co Ymg6fdoxu1 18 30の動画アップをお待ち下さい 入試問題 数学 ドラゴン桜 連立方程式 高校数学



連立方程式の問題です これのx Y Z Qの答えと求め方教えてくだ Yahoo 知恵袋




三元連立方程式 1 中2数学 Youtube




高校数学iの問題です 応用 3元連立方程式を解けという問題で Clear




この連立方程式がどうしても解けないです Clear
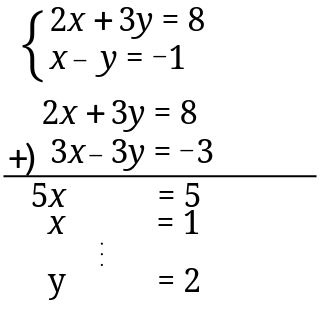



途中式を書くとケアレスミスが増える 連立方程式では常識とは逆を行け さびねこ中学校



連立方程式の行列解




Python 3 X 多元非線形連立方程式のpythonを用いた解法について Teratail




連立方程式 1 代入法と加減法 バカでもわかる 中学数学



1




Left 3right 1 Begincase Descubre Como Resolverlo En Qanda




4begincasesxyz13x Y2z73xy Lihat Cara Penyelesaian Di Qanda




連立方程式を解く 置換法と加算法 代数参照 教科書 21




高校数学 3つの解から3次方程式の作成 3変数対称式の連立方程式 受験の月
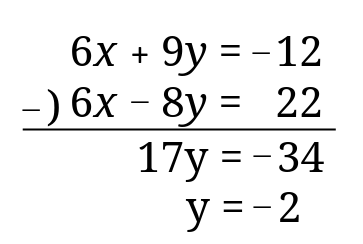



連立方程式を見直ししてもうっかりケアレスミスをしてしまうときの対処法 さびねこ中学校



Seqi Pukiwiki




3分でわかる 連立方程式の代入法と加減法をわかりやすく 合格サプリ



Q Tbn And9gcrxeqtkfzspr84pbplx9xl09lwn 7v64y00sc7qxffojd2h H0u Usqp Cau



Excel の行列計算による連立方程式の解き方



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス



0 件のコメント:
コメントを投稿